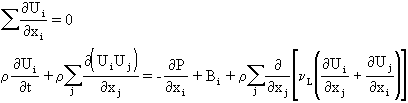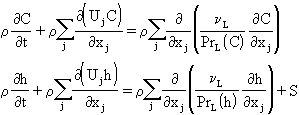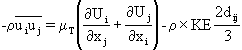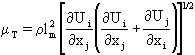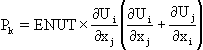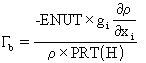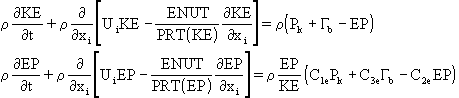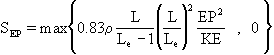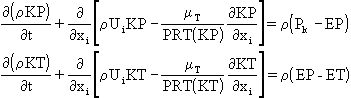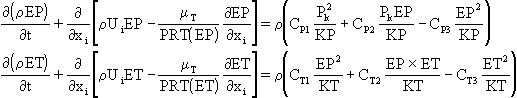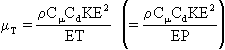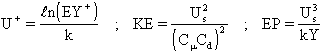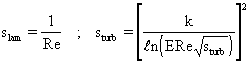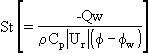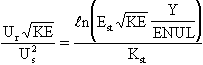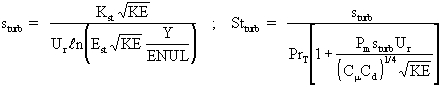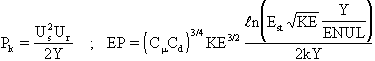Nis 10 2012

Türbülans Modelleri | Turbulence Models

Original page: >> http://www.cham.co.uk/phoenics/d_polis/d_lecs/general/turb.htm

—————————————————————–

 

Encyclopaedia Index

TURBULENCE MODELS

Contents

 

Nature Of Turbulence

Turbulence is a kind of fluid motion which is:

  • UNSTEADY and highly IRREGULAR in space and time
  • 3-DIMENSIONAL (even if the mean flow is only 2D)
  • always ROTATIONAL and at HIGH REYNOLDS NUMBERS
  • DISSIPATIVE (energy is converted into heat due to viscous stresses)
  • strongly DIFFUSIVE (rapid mixing)

Turbulent fluctuations can generate rates of momentum transfer far greater than those due to molecular diffusion.

The turbulent motion has a wide spectrum of eddy sizes, and large and small eddies can coexist in the same volume of fluid.

The LARGEST eddies are associated with LOW frequency fluctuations, as large as the dimensions of the flow, and responsible for most of the momentum transport. The SMALLEST eddies are associated with HIGH frequency fluctuations, and are determined by viscous forces.

 

Simulation of Turbulent Flows

It is widely accepted that the Navier-Stokes (NS) equations together with the continuity equation comprise a closed set of equations, the solution of which provides a valid description of laminar and turbulent flows.

For an incompressible flow, these equations are:

The equations for a scalar quantity C, such as species concentration, and an energy variable, such as enthalpy h, are:

It is possible, in principle, to simulate any turbulent flow by solving the foregoing exact equations with appropriate boundary conditions using suitable numerical procedures such as embodied in PHOENICS.

Such a calculation is called DIRECT NUMERICAL SIMULATION, but in practice it is rarely done.

This is because of the need to represent all eddies from the smallest scale, corresponding to the dissipative motions, to the largest scale, corresponding to the largest dimension. Further, the time step chosen for the simulations must be sufficiently small to resolve the fastest fluctuations.

For the values of Reynolds numbers encountered in practical engineering flows, the computational effort is prohibitive.

There are essentially two alternative routes for the prediction of turbulent flows:

LES involves:

  • the solution of the 3D time-dependent NS equations
  • direct simulation of the large-scale motion; and
  • use of a sub-grid-scale (SGS) model for turbulence of scales smaller than the computational grid spacing.

The advantages of LES arise from the fact that the large eddies, which are hard to model in a universal way, are simulated directly.

The application of LES to practical flows has been limited because of:

prohibitive expense at high Reynolds number;

the difficulties in specifying initial and boundary conditions; and

the need to perform 3D time-dependent simulations, even if the flow is 2D and statistically stationary!

 

Turbulence Modelling

Engineers are not concerned with all the details of the turbulent motion, but rather with its effects on the gross properties of the flow. Consequently, there is no need to solve for the INSTANTANEOUS variables if AVERAGED variables are all that is required.

The instantaneous variables are decomposed into MEAN and FLUCTUATING quantities:

where the mean values are obtained by averaging over a time scale, dt, which is long compared to that of turbulent motion, and in unsteady problems small compared with the unsteadiness of the mean motion.

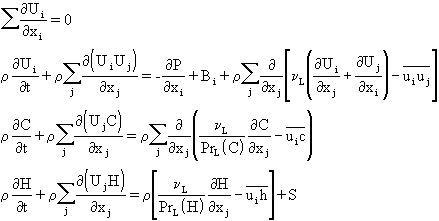
The definitions of instantaneous quantities are substituted into the equations of the INSTANTANEOUS MOTION, which are then averaged to produce the equations of the MEAN MOTION.

For an incompressible flow, the AVERAGED equations are:

The statistical-averaging process has introduced unknown turbulent correlations into the mean-flow equations which represent the turbulent transport of momentum, heat and mass – the REYNOLDS STRESSES and FLUXES. In general, there are: 

  • 6 Reynolds stress components: -uiuj
  • 3 Reynolds enthalpy flux components: -uih
  • 3 Reynolds mass flux components: -uic

A TURBULENCE MODEL can be described as a set of relations and equations needed to determine the unknown turbulent correlations that have arisen from the averaging process.

Turbulence models of various complexity have been developed, and with very few exceptions, they can be classified as EDDY-VISCOSITY MODELS or REYNOLDS-STRESS MODELS.

In EDDY-VISCOSITY MODELS, the unknown correlations are assumed to be proportional to the spatial gradients of the quantity they are meant to transport.

In REYNOLDS-STRESS MODELS, the unknown correlations are determined directly from the solution of differential transport equations in which they are the dependent variables.

 

Eddy-Viscosity Concept

Most turbulence models use the eddy-viscosity concept to determine the Reynolds stresses from:

where is the eddy viscosity and KE is the turbulent kinetic energy.

is NOT a fluid property; it depends on the state of turbulence and must be determined by the turbulence model.

For enthalpy and mass transfer, the Reynolds fluxes are determined from:

where and are turbulent Prandtl and Schmidt numbers, which are approximately unity.

For dimensional reasons, is proportional to:

where C is an empirical constant, and Vs and Ls are turbulence velocity and length scales which characterize the LARGE-SCALE turbulent motion.

The simplest turbulence model is one which uses a constant value for the eddy viscosity. It is often convenient to use this very simple model whilst the main features of the CFD simulation are being put together. A more accurate turbulence model can be introduced at a later stage. 

A reasonable value of the kinematic eddy viscosity, , can be estimated by taking: C=0.01; Vs as a typical mean-flow velocity, say the bulk value; and the length scale Ls as ~10% of the flow width.

 

Classification Of Turbulence Models 

  • ZERO-EQUATION MODELS- Vs and Ls are calculated directly from the local mean flow quantities (e.g. Prandtl's mixing-length model).
  • ONE-EQUATION MODELS- Vs is calculated from a suitable transport equation, usually the turbulent kinetic energy, KE, and the length scale, Ls, is prescribed empirically (e.g. Prandtl's k-L model).
  • TWO-EQUATION MODELS- Vs and Ls are both calculated from transport equations, usually KE and its dissipation rate EP.
  • REYNOLDS-STRESS/FLUX TRANSPORT MODELS- These are models involving the solution of transport equations for the Reynolds stresses and fluxes, together with a transport equation for the length scale, usually EP.
  • ALGEBRAIC STRESS/FLUX MODELS- These models simplify the stress/flux transport equations to provide algebraic expressions for the turbulent correlations, which are then solved together with a 2-equation model.

 

Zero-Equation Models

Constant Viscosity Model

Vs is a typical velocity scale, Ls a typical length scale, and C is a constant the order of 0.01.

In PHOENICS: set ENUT to a constant value in the Q1 file.

The velocity scale can be taken to be an average domain velocity, and the length scale approximately 10% of the domain size.

In duct flows, a useful formula is: where the friction factor .

It is often convenient to use this very simple model whilst the main features of the simulation are being put together. A more accurate turbulence model can be activated once you are satisfied that other aspects of the flow are well represented.

 

Prandtl Mixing-Length Model

Prandtl's mixing-length model calculates from:

where lm=mixing length and has to be prescribed. Near a wall ; in free flows ; in a duct, Nikuradse's lm-formula is usually appropriate; in a boundary layer, a lm ramp-distribution is often suitable.

The model is:

  • suitable for simple shear-layer-dominated or pressure-driven flows
  • simple and computationally economical
  • unsuitable for complex flows because it is very difficult to estimate the distribution of the mixing length
  • cannot account for the transport effects of turbulence

In PHOENICS set: ENUT = GRND2 ; EL1 = GRND1, 2, 3… as appropriate; and GENK = T to activate calculation of the velocity derivatives.

 

LVEL TURBULENCE MODEL

The LVEL turbulence model is applicable only when walls are present, and it calculates ENUT via Spalding's law of the wall, which covers the entire laminar and turbulent regimes, thus:

where k=0.41, E=8.6, and . The local parameter X+ is determined iteratively from a non-linear expression involving k, E and the local Reynolds number Re, which is based on a typical local velocity and the normal distance to the nearest wall WDIS.

WDIS is calculated from an algebraic function of a scalar variable L and its gradient, while L itself is obtained by solving:

with L fixed to zero in solids.

TURMOD(LVEL) activates the LVEL turbulence model.

The model is useful for situations in which fluid flows through spaces cluttered with many solid objects (electronics cooling). In such cases the grid density between nearby solids is often too coarse for the k-e model to be meaningfully employed.

 

One-Equation Models

PRANDTL'S K-L MODEL

Prandtl's one-equation model may be summarized as follows:

where:

gi is the gravity vector,  lm has to be prescribed, and the empirical constants are:

Cm=0.5478; Cd=0.1643; and PRT(KE)=1.0.

1-equation models account for Vs transport, which is important in developing and relaxing flows, and in flows controlled by free-stream turbulence.

The main shortcomings concern Ls: its transport is not considered, which is important in separated flows; and it must be prescribed, which is difficult for complex flows. The trend has been to use 2-equation models.

TURMOD(KLMODL) activates the k-L model, and buoyancy production is introduced into the model by the following additional PIL commands:

PATCH(KEBUOY,PHASEM,1,NX,1,NY,1,NZ,1,LSTEP)
COVAL(KEBUOY,KE,GRND4,GRND4)

The formula for Ls must be selected by setting EL1 to one of the built-in options.

 

Two-Equation Models

The velocity scale, Vs, is calculated from solution of a transport equation for KE.

The dependent variable of the 2nd transport equation is not usually Ls itself, but rather the variable .

There are many possible choices for the second turbulence variable, resulting in different values of m and n. These include:

  • Harlow-Nakamaya KE-EP model + variants m=1.5 n=-1.0
  • Saffman-Spalding KE-VOSQ model m=1.0 n=-2.0
  • Kolmogorov KE-OMEG model m=0.5 n=-1.0
  • Rotta KE-KE*Ls model m=1.0 n=1.0

The KE-EP model has proved the most popular, mainly because it does not require a near-wall correction term.

 

THE KE-EP MODEL

The standard high-Re form of the KE-EP model employs the following turbulence transport equations:

The kinematic turbulent (or eddy) viscosity and the length scale, Ls are given by:

;

The model constants are: Cm=0.5478; Cd=0.1643; PRT(KE)=1.0; PRT(EP)=1.314; C1e=1.44, C2e=1.92 and C3e=1.0.

The buoyancy production is < 0 for stably-stratified layers, so that KE is reduced and turbulence damped. For unstably-stratified layers, is positive and turbulence is augmented.

The constant C3e has been found to depend on the flow situation. It should be close to zero for stably-stratified flow, and close to 1.0 for unstably-stratified flows. 

The default value of C3eis 1.0, and it can be changed by using:

SPEDAT(SET,KEBUOY,GCEB,R,0.3).

TURMOD(KEMODL) activates the KE-EP model, and may be introduced by the following additional PIL commands:

PATCH(KEBUOY,PHASEM,1,NX,1,NY,1,NZ,1,LSTEP)
COVAL(KEBUOY,KE,GRND4,GRND4)
COVAL(KEBUOY,EP,GRND4,GRND4)

C3e=0 may be effected by simply not using the COVAL statement.

Two-equation models account for transport effects of Vs and Ls, and the distribution of Ls is determined by the model. The model forms a good compromise between generality and economy of use for many CFD problems.

The models have limited universality, mainly due to the rather simple modelling of the creation and destruction of the Ls-determining variable. Hence, the large number of k-e variants involving a modified EP equation.

The use of the eddy-viscosity concept imposes isotropy, i.e. the same values are taken for the various Reynolds stresses. This assumption may be too simple, for example when body forces are present (gravity, rotation, magnetic fields) and in flows with streamline curvature.

The two-equation models presented thus far are valid only at high turbulent Reynolds numbers, and therefore they are not valid in the near-wall viscosity-affected region.

 

The Yap KE-EP Model

For separated and reattaching flows, the standard KE-EP model encounters difficulties, e.g. as boundary layers develop towards separation the predicted near-wall length scales become too large, and the length of separation regions is underpredicted in flows past steps and obstacles.

Several variants of the KE-EP model have been proposed for dealing with this deficiency, including the Yap [1987] modification to the EP-equation:

where and , with , YN is the distance from the wall and .

The correction can produce substantial improvements, particularly in heat-transfer predictions in separated flows.

The Yap correction is activated by using TURMOD(KEMODL-YAP).

 

The RNG KE-EP Model

The KE-EP model is known to be too dissipative – the turbulent viscosity in recirculations tends to be too high, thus damping out vortices.

TURMOD(KERNG) selects the RNG k-e model. This attempts to correct this deficiency by using slightly different constants, and by adding the following volumetric source term to the EP equation:

where: ; ; ; and the dimensionless parameter .

The changes to the model constants are: PRT(KE)=0.7194, PRT(EP)=0.7194,

Although very good for separation and reattachment, its predictions for jets and plumes are inferior to the standard model.

 

The Chen-Kim KE-EP Model

TURMOD(KECHEN) selects the modified KE-EP model of Chen and Kim, which is another attempt to cure the over-dissipative nature of the KE-EP model.

This variant of the KE-EP model uses slightly different constants and introduces an additional source term into the EP equation, i.e.:

where C4e=0.25. The changes to the model constants are: PRT(KE)=0.75, PRT(EP)= 1.15, C1e=1.15 and C2e=1.9.

It predicts reattachment points and vortices almost as well as the RNG version, but preserves the good behavior for jets and plumes of the standard version.

A low-Re extension can be selected by TURMOD(KECHEN-LOWRE).

 

Two-Scale KE-EP Model

TURMOD(TSKEMO) selects the two-scale split-spectrum KE-EP model.

This model splits the turbulence-energy spectrum into 2 regions, namely the 'production' (P) region and the 'transfer' (T) region. Spectral equilibrium is assumed between the T region and the region in which turbulence is dissipated, i.e. the dissipation (D) region.

Two transport equations are solved for each of these regions, namely: KP and EP for the P region; and KT and ET for the T region. EP is the energy transfer rate from the P to T range and ET is the dissipation rate.

The total turbulent kinetic energy KE = KP + KT.

The two-scale model embodied in PHOENICS employs variable partitioning of the spectrum, so that the location of the partition (the value of KP/KT ) is calculated automatically by the model.

The transport equations for KP and KT are:

The transport equations for EP and ET are given by:

The turbulent eddy viscosity is computed from:

where and .

The functional relationship for determines the location of the partition between the P and T regions. Note that for turbulent flows in local equilibrium, Pk=ET and ET=EP so that .

The model constants are: PRT(KP)=0.75, PRT(EP)=1.15, PRT(KT)=0.75, PRT(ET)=1.15, CP1=0.21, CP2=1.24, CP3=1.84, CT1=0.29, CT2=1.28 and CT3=1.66.

The model may be used in combination with equilibrium (GRND2) or non-equilibrium (GRND3) wall functions.

The advantage of the 2-scale KE-EP model lies in its capability to model the cascade process of turbulent kinetic energy; and to resolve the details of complex turbulent flows better than the standard k-e model.

The disadvantage is that it requires 4 turbulence transport equations, as opposed to the 2 equations required for the standard k-e model.

The recommendation is that the standard k-e model or one of its variants be used in the first instance. However, in cases where these models are clearly giving poor predictions the 2-scale model should be used to see whether better predictions can be obtained.

Documentation: see the PHENC entry TWO-SCALE KE-EP TURBULENCE MODEL.

Library Examples: see cases T400-T406 inclusive.

 

Reynolds-Stress Transport Model

In general the Reynolds-stress transport model (RSTM) involves the solution of the following turbulence transport equations:

  • 3 normal stresses
  • 3 shearing stresses
  • The dissipation rate EP
  • 3 enthalpy fluxes, and 3 mass fluxes per scalar variable

The 3 normal stresses are always solved, but the shearing stresses are solved only when the appropriate velocity components are solved.

The Reynolds-stress transport equations may be written in the following symbolic tensor form:

Tij + Cij = Dij + Pij + Rij – Eij

where Tij=transience, Cij=convection, Dij=diffusion, Pij=production, Rij=redistribution and Eijdissipation.

The Rij term is the most important term requiring closure in the RSTM. It is commonly known as the pressure-strain term, and PHOENICS provides for 3 different closure models which are selected by IRSMHM, as follows:

  • IRSMHM = 0 selects the IPM model (the default )
  •             = 1 '' '' QIM ''
  •             = 2 '' '' IPY ''

The IPM and QIM models are the most commonly used in the literature, while the IPY model performs similarly but offers advantages for swirl flows.

These pressure-strain models require wall-correction terms which are provided by PHOENICS as default through the TURMOD command. The corrections account for wall effects on the redistribution process.

The RSTM itself is activated from the Q1 file by the PIL command

TURMOD(REYSTRS,DTFS,WALL1,WALL2,…)

The wall patches WALL1, WALL2, etc. must be previously defined through laminar wall PATCH and COVAL settings for the velocity variables.

The TURMOD command will then:

  1. create COVAL settings for the velocities and EP using GRND2 wall functions
  2. create PATCH and COVAL settings for the stress-equation variables so as to represent the wall-damping sources associated with the chosen pressure-strain model
  3. create RELAX commands for all SOLVEd variables with a false time step of DTFS

The TURMOD command also activates solution of: the dissipation rate EP; the normal stresses U2RS, V2RS, W2RS; and, as appropriate, the shearing stresses UVRS, UWRS and VWRS.

When heat and/or mass transfer is activated the default is that the turbulent fluxes of energy and scalars are represented by a simple gradient-diffusion model through the default setting IRSMSM=0, i.e.

where and =0.255.

The generalized gradient-diffusion model can be activated by setting IRSMSM=1, in which case the Reynolds fluxes are computed from:

where the coefficient Ct=0.3. The command IRSMSM must appear before the TURMOD command in the Q1 file.

The full Reynolds-flux transport model can be activated by setting IRSMSM=2 before the TURMOD command in the Q1 file. The flux transport equations may be written in the following symbolic tensor form:

where Ti=transience, Ci=convection, Di=diffusion, Pi=production, and Ri=pressure-scrambling. The Ri term requires wall-correction terms which are provided by PHOENICS as default through the TURMOD command.

If H1 or TEM1 are stored, TURMOD automatically sets:

  • STORE(UTRS) if NX > 1
  • STORE(VTRS) if NY > 1
  • STORE(WTRS) if NZ > 1 and .NOT. PARAB

Likewise, if SC1, SC2, SCn, etc., are STOREd, storage is provided as appropriate for USC1, USC2, USCn, VSC1, VSC2, VSCn, WSC1, WSC2, WSCn etc.

If IRSMSM=2 the procedure is the same excepting that SOLVE replaces STORE because transport equations will now be solved for each of the individual flux components.

In addition, wall damping sources are created for these components, and if U1 is SOLVEd and NX=1 then UTRS, USC1, USC2, USCn are also SOLVEd.

The advantage of the RSTM is that it provides a more rigorous and realistic approach, and it captures anisotropic effects automatically.

However, RSTMs are much more complex than eddy-viscosity models, and they are computationally more expensive and less stable.

Documentation: see the PHENC entry: REYNOLDS-STRESS TURBULENCE MODEL.

Library Examples: see cases T600-T609 inclusive.

 

Near-Wall Approaches

The wall no-slip condition ensures that over some region of the wall layer, viscous effects on the transport processes must be large.

The representation of these processes within a CFD model raises 2 problems:

  1. How to account for viscous effects at the wall.
  2. How to resolve the rapid variation of flow variables which occurs within this region, without using a very fine computational mesh.

There are two methods:

  • the WALL-FUNCTION method  and
  • the LOW-REYNOLDS-NUMBER method

For extensive documentation see the PHENC entries: WALL_FUNCTIONS; and LOW-REYNOLDS-NUMBER TURBULENCE MODELS.

Wall-Function Method

The viscous sublayer is bridged by employing empirical formulae to provide near-wall boundary conditions for the mean flow and turbulence transport equations.

These formulae connect the wall conditions (e.g. the wall shear stress) to the dependent variables at the near-wall grid node which is presumed to lie in fully-turbulent fluid.

Strictly, wall functions should be applied to a point whose Y+ value is in the range 30 < Y+ < 130, where and US is the friction velocity. The user may elicit printout of Y+ in the RESULT file by setting YPLS=T or WALPRN=T in the Q1 file. If in addition, STORE(YPLS) appears UP> is written to both the PHI and RESULT files.

The advantages of this approach are that it escapes the need to extend the computations right to the wall, and it avoids the need to account for viscous effects in the turbulence model.

Equilibrium Wall Functions

Equilibrium wall functions use log-law formulae at near-wall grid point, and are invoked by setting WALLCO=GRND2 in the Q1 file before the WALL or CONPOR command :

where , E=8.6, k=0.41 and Ur is the resultant velocity.

Wall friction is introduced via momentum source terms involving the friction factor ; where

s=max<sturb,slam> and

and the local Reynolds number .

Roughness effects can be taken into account by setting WALLA to the equivalent sand-grain roughness height in the Q1 input file. PHOENICS then takes E as a function of the roughness Reynolds number.

For heat and mass transfer, the wall flux QW of the variable f is calculated via the Stanton number

St is determined from St=max<Stturb , Stlam>, with:

with . PrT and PrL denote the turbulent and laminar Prandtl/Schmidt numbers.

In PHOENICS the equilibrium wall functions are activated by:

WALL(INAME,AREA,IF,IL,JF,JL,KF,KL,1,LSTEP)
COVAL(NAME,H1,GRND2,H1WALL)

or

CONPOR(NAME,0,’type’,-IF,-IL,-JF,-JL,-KF,-KL)

The '-' flags that wall functions are to be generated on that surface.

 

Non-Equilibrium Wall Functions

A generalization of the 'equilibrium' treatment to non-equilibrium conditions is also in PHOENICS, which may be invoked by setting WALLCO=GRND3 in the Q1 file before the WALL or CONPOR command.

The log-law is extended to non-equilibrium conditions, as follows:

where and .

The turbulent friction factor and Stanton number are now given by:

The value of KE at the near-wall point is calculated from its own transport equation with the diffusion of energy to the wall being set equal to zero.

The mean values of Pk and EP over the near-wall cell are represented as:

in the transport equation for KE.

However, in the formula for the near-wall eddy viscosity, EP is calculated from .

The non-equilibrium wall functions will give better predictions of heat transfer coefficients at a reattachment point.

 

Fully-rough wall functions

PHOENICS also provides wall functions that are suitable for a fully-rough near-wall layer in local equilibrium, defined in terms of the effective roughness height, as for example in the atmospheric boundary layer.

These wall functions may be activated by setting WALLCO=GRND5 in the Q1 file before the WALL or CONPOR command.

These wall functions are the same as those described above for GRND2 equilibrium turbulent wall functions, except for the form of the logarithmic wall law, which is now given by:

               Ur/UTAU = LN(Y/Y0)/k

where Y0 is the effective roughness height.

This height is related to the size of the roughness elements on the surface, e.g. a typical value for grass is 0.01m, whereas for forest it is about 1m.

For heat and mass transfer, the Stanton number is computed from a modified Reynolds analogy, i.e. St=s/Prt.

Library example: see case T306 for a simple example of an atmospheric boundary layer.

Low-Reynolds-Number Models

The alternative to wall functions is to use a fine-grid analysis in which computations are extended through the viscosity-affected sublayer close enough to the wall to allow laminar-flow boundary-conditions to be applied.

The low-Re extension of Lam and Bremhorst (LB) may be applied to the standard KE-EP model, and also the Chen-Kim modified KE-EP model, by the PIL commands TURMOD(KEMODL-LOWRE) and TURMOD(KECHEN-LOWRE). The Yap correction to the LB model is activated by using TURMOD(KEMODL-LOWRE-YAP).

The two-layer low-Reynolds-number k-e model is activated by the PIL command TURMOD(KEMODL-2L). This model employs the high-Re k-e model away from the wall in fully-turbulent regions, and a one-equation k-L model in the near-wall viscosity-effected region.

These models differ from the standard k-e model in that the model coefficients are functions of the local turbulent Reynolds number.

When applicable, the 2-layer model is to be preferred to the LB model because it improves convergence behavior, requires less mesh points, and it introduces the fairly well established near-wall Ls distribution.

The disadvantage of low-Re models is that a very fine grid is required in each near-wall zone. Consequently, the computer-storage and runtime requirements are much greater than those of the wall-function approach.

Convergence can be difficult with low-Re k-e models due to the problem of stiffness. Care must be taken to ensure good numerical resolution in the near-wall region so as to capture the rapid variation in variables.

Documentation: see PHENC entries: LOW-REYNOLDS-NUMBER TURBULENCE MODELS; LAM-BREMHORST KE-EP TURBULENCE MODEL; TWO-LAYER KE-EP TURBULENCE MODEL.

Library examples: see cases 296 and T205 to T214 inclusive.

 

Boundary Conditions

Attention is restricted to boundary conditions for the KE-EP model.

  • PLANE OR AXIS OF SYMMETRY: The normal gradients are zero for both KE and EP which is the default condition in PHOENICS.
  • WALL BOUNDARIES: Wall function, or a low-Reynolds-number approach.
  • FREE SURFACES: In many cases, a free surface can be considered to a first approximation as a symmetry plane.
  • FREE (ENTRAINMENT) BOUNDARIES: A fixed-pressure condition is employed at free boundaries, which involves prescribing free stream values for KE and EP. If the ambient stream is assumed to be free of turbulence, then KE and EP can be set to negligibly small values. However, it is advisable to ensure that these values are such that ENUT ~ ENUL.
  • PRESCRIBED INLET CONDITIONS: The inlet values of KE and EP are often unknown, and the advice is to take guidance from experimental data for similar flows. The simplest practice is to assume uniform values of KE and EP computed from:

           

where I is the turbulent intensity (typically in the range 0.01 < I < 0.05) and LM ~ 0.1H, where H is a characteristic inlet dimension, say the hydraulic radius of the inlet pipe.

 

Convergence Advice

Attention is restricted to convergence advice for the KE-EP model.

If convergence is problematic, and the boundary conditions are correct, the guidelines given below should be consulted.

INITIAL VALUES:

  • Although not often responsible for poor convergence, the use of unrepresentative initial KE and EP values can lead to problems.
  • In general, the default values of 1.E-10 are unlikely to be physically sensible values, except perhaps in transient calculations with a stagnant initial field.
  • A simple expedient is to set FIINIT(KE) and FIINIT(EP) to values computed using the formulae given above for inlet streams. The intensity I and dimension H can either be based on an inlet stream, or alternatively on the flow domain itself.

RELAXATION:

  • The use of linear relaxation is recommended with values, typically, in the range 0.2 to 0.4, e.g., RELAX(KE,LINRLX,0.3).
  • If inertial relaxation is used, then strictly the false time-step should be based on a representative turbulence timescale KE/EP. Since this is difficult to quantify, one either uses linear relaxation or uses the same false time-step as for velocities.
  • It is also possible to apply linear under-relaxation on the turbulent kinematic viscosity, provided that STORE(ENUT) appears in the Q1 file. Thus, for example, RELAX(ENUT,LINRLX,0.5) would be a typical setting. However, this is recommended as a last resort.
  • If ENUT relaxation is used, it is recommended that the user set KELIN=3, as with other values of KELIN the KE and EP sources are cast in terms of ENUT on the presumption that no linear relaxation is applied. KELIN is described in the next panel.

SOURCE-TERM LINEARIZATION:

  • The production and dissipation source terms in the KE and EP transport equations are linearized in PHOENICS so as to provide an implicit under-relaxation of these variables.
  • KELIN determines the linearization practice used, and although these practices make no difference to the final solution, they can considerably alter convergence rates.
  • KELIN can take the values 0 (the default), 1, 2 and 3.
  • If convergence is proving difficult with KELIN=0, then experience has shown that more often than not, KELIN=1 or KELIN=3 will promote convergence.
  • For more detailed information, see the PHENC entry KELIN.

 

 

Encyclopaedia Entries

All turbulence models are documented in the Encyclopaedia under 'Turbulence' and also on-line at the following address:

            http://www.cham.co.uk/phoenics/d_polis/d_enc/turmod/enc_tu.htm

Relevant individual "Encyclopedia" entries include:

 

Library Examples

Examples of turbulent flow can be found in many sections of the Library. In particular, attention should be paid to:

Core Library Section 3 – Parabolic Flows

Core Library Section 4 – 2 & 3 Dimensional Elliptic Flows

Advanced Turbulence models Library

The single-slab solver cases are particularly worthy of study, as they are very quick to run, and demonstrate well how the different models perform.

 

References

 

On turbulence:

  • H. Tennekes & J. L. Lumley, 'A first course in turbulence', 6th Edition, MIT Press, (1972).
  • J. O. Hinze, 'Turbulence', 2nd Edition, McGraw- Hill, New York, (1975).
  • P. Bradshaw, 'An introduction to turbulence and its measurement’, Pergamon Press, (1975).
  • P. Bradshaw, 'Turbulence', Topics in Applied Physics, Vol.12, SpringerVerlag, (1978).

On turbulence modelling:

  • Launder B.E. and Spalding D.B., 'Mathematical Models of Turbulence', Academic Press, London (1972)
  • W. Rodi, 'Turbulence models and their applications in hydraulics: A state of the art review', Book publication of IAHR, Delft, The Netherlands,(1980).
  • 'Introduction to the modelling of turbulence', VKI Lecture Series 1991-02, March 18-21, VKI, Belgium, (1991).
  • Launder, B. E., 'Second-moment closure and its use in modelling turbulent industrial flows.', Int. J. Num. Methods in Fluids, Vol. 9, p963, (1989b).
  • Leschziner, M. A., 'Modelling engineering flows with Reynolds stress turbulence closure.', J. Wind Engng. & Industrial Aerodynamics.', Vol. 35, p21, (1990).
  • Wilcox, D.C., 'Turbulence Modelling for CFD', DCW Industries, (1998).
  • Pope, S.B., 'Turbulent Flows', (2000)
Related articles

Ayhan Baydır